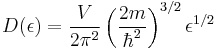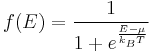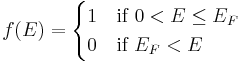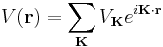Electronic band structure
In solid-state physics, the electronic band structure (or simply band structure) of a solid describes those ranges of energy, called energy bands, that an electron within the solid may have ("allowed bands"), and ranges of energy called band gaps ("forbidden bands"), which it may not have. Band theory models the behavior of electrons in solids, by postulating the existence of energy bands. It successfully uses a material's band structure to explain many physical properties of solids, such as electrical resistivity and optical absorption. Bands may also be viewed as the large-scale limit of molecular orbital theory. A solid creates a large number of closely spaced molecular orbitals, which appear as a band. Band structure derives from the dynamical theory of diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and Bravais lattice.
Contents |
Why bands occur in materials
The electrons of a single isolated atom occupy atomic orbitals, which form a discrete set of energy levels. If several atoms are brought together into a molecule, their atomic orbitals split, as in a coupled oscillation. This produces a number of molecular orbitals proportional to the number of atoms. When a large number of atoms (of order ×1020 or more) are brought together to form a solid, the number of orbitals becomes exceedingly large. Consequently, the difference in energy between them becomes very small. Thus, in solids the levels form continuous bands of energy rather than the discrete energy levels of the atoms in isolation. However, some intervals of energy contain no orbitals, no matter how many atoms are aggregated, forming band gaps.
Within an energy band, energy levels form a near continuum. First, the separation between energy levels in a solid is comparable with the energy that electrons constantly exchange with phonons (atomic vibrations). Second, it is comparable with the energy uncertainty due to the Heisenberg uncertainty principle, for reasonably long intervals of time. As a result, the separation between energy levels is of no consequence.
Several approaches to finding band structure are discussed below.
Basic concepts
Any solid has a large number of bands. In theory, a solid can have infinitely many bands (just as an atom has infinitely many energy levels). However, all but a few of these bands lie at energies so high that any electron that attains those energies will escape from the solid. These bands are usually disregarded.
Bands have different widths, based upon the properties of the atomic orbitals from which they arise. Also, allowed bands may overlap, producing (for practical purposes) a single large band.
Figure 1 shows a simplified picture of the bands in a solid that allows the three major types of materials to be identified: metals, semiconductors and insulators.
Metals contain a band that is partly empty and partly filled regardless of temperature. Therefore they have very high conductivity.
The lowermost, almost fully occupied band in an insulator or semiconductor, is called the valence band by analogy with the valence electrons of individual atoms. The uppermost, almost unoccupied band is called the conduction band because only when electrons are excited to the conduction band can current flow in these materials. The difference between insulators and semiconductors is only that the forbidden band gap between the valence band and conduction band is larger in an insulator, so that fewer electrons are found there and the electrical conductivity is lower. Because one of the main mechanisms for electrons to be excited to the conduction band is due to thermal energy, the conductivity of semiconductors is strongly dependent on the temperature of the material.
This band gap is one of the most useful aspects of the band structure, as it strongly influences the electrical and optical properties of the material. Electrons can transfer from one band to the other by means of carrier generation and recombination processes. The band gap and defect states created in the band gap by doping can be used to create semiconductor devices such as solar cells, diodes, transistors, laser diodes, and others.
Symmetry
A more complete view of the band structure takes into account the periodic nature of a crystal lattice using the symmetry operations that form a space group. The Schrödinger equation is solved for the crystal, which has Bloch waves as solutions:
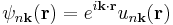 ,
,
where k is called the wavevector, and is related to the direction of motion of the electron in the crystal, and n is the band index, which simply numbers the energy bands. The wavevector k takes on values within the Brillouin zone (BZ) corresponding to the crystal lattice, and particular directions/points in the BZ are assigned conventional names like Γ, Δ, Λ, Σ, etc. These directions are shown for the face-centered cubic lattice geometry in Figure 2.
The available energies for the electron also depend upon k, as shown in Figure 3 for silicon in the more complex energy band diagram at the right. In this diagram the topmost energy of the valence band is labeled Ev and the bottom energy in the conduction band is labeled Ec. Note that for silicon, the top of the valence band is not directly below the bottom of the conduction band (Ev is for an electron traveling in direction Γ, Ec in direction X), so silicon is called an indirect gap material. For an electron to be excited from the valence band to the conduction band within an indirect gap material, it needs something to give it both energy Ec – Ev and a change in direction/momentum. In other semiconductors (for example III-V materials, such as GaAs) both Ec and Ev are at Γ, and therefore these materials are direct gap materials (no momentum change required). Direct gap materials benefit the operation of semiconductor laser diodes.
Anderson's rule is used to align band diagrams between two different semiconductors in contact.
Band structures in different types of solids
Although electronic band structures are usually associated with crystalline materials, quasi-crystalline and amorphous solids may also exhibit band structures. However, the periodic nature and symmetrical properties of crystalline materials makes it much easier to examine the band structures of these materials theoretically. In addition, the well-defined symmetry axes of crystalline materials makes it possible to determine the dispersion relationship between the momentum (a 3-dimension vector quantity) and energy of a material. As a result, virtually all of the existing theoretical work on the electronic band structure of solids has focused on crystalline materials.
Solid state properties and the Pauli principle
In conductors and semi-conductors, free electrons have to share entire bulk space. Thus, their energy levels stack up, creating band structure out of each atomic energy level. In strong conductors (metals) electrons are so degenerate that they can not even contribute much to the thermal capacity of a metal. Many mechanical, electrical, magnetic, optical and chemical properties of solids are the direct consequence of the Pauli exclusion principle.
Density of states
While the density of energy states in a band could be very large for some materials, it may not be uniform. It approaches zero at the band boundaries, and is generally highest near the middle of a band. The density of states for the free electron model in three dimensions is given by,
Filling of bands
Although the number of states in all of the bands is effectively infinite, in an uncharged material the number of electrons is equal only to the number of protons in the atoms of the material. Therefore not all of the states are occupied by electrons ("filled") at any time. The likelihood of any particular state being filled at any temperature is given by Fermi-Dirac statistics. The probability is given by the following expression:
where:
- kB is Boltzmann's constant,
- T is the temperature,
- µ is the chemical potential (in semiconductor physics, this quantity is more often called the "Fermi level" and denoted EF).
The Fermi level naturally is the level at which the electrons and protons are balanced.
At T=0, the distribution is a simple step function:
At nonzero temperatures, the step "smooths out", so that an appreciable number of states below the Fermi level are empty, and some states above the Fermi level are filled.
Theory of band structures in crystals
The ansatz is the special case of electron waves in a periodic crystal lattice using Bloch waves as treated generally in the dynamical theory of diffraction. Every crystal is a periodic structure which can be characterized by a Bravais lattice, and for each Bravais lattice we can determine the reciprocal lattice, which encapsulates the periodicity in a set of three reciprocal lattice vectors (b1,b2,b3). Now, any periodic potential V(r) which shares the same periodicity as the direct lattice can be expanded out as a Fourier series whose only non-vanishing components are those associated with the reciprocal lattice vectors. So the expansion can be written as:
where K = m1b1 + m2b2 + m3b3 for any set of integers (m1,m2,m3).
From this theory, an attempt can be made to predict the band structure of a particular material, however most ab initio methods for electronic structure calculations fail to predict the observed band gap.
Nearly free electron approximation
In the nearly-free electron approximation, interactions between electrons are completely ignored. This approximation allows use of Bloch's Theorem which states that electrons in a periodic potential have wavefunctions and energies which are periodic in wavevector up to a constant phase shift between neighboring reciprocal lattice vectors. The consequences of periodicity are described mathematically by the Bloch wavefunction:
where the function 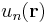 is periodic over the crystal lattice, that is,
is periodic over the crystal lattice, that is,
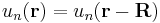 .
.
Here index n refers to the n-th energy band, wavevector k is related to the direction of motion of the electron, r is position in the crystal, and R is location of an atomic site.[1]
The NFE model works particularly well in materials like metals where distances between neighbouring atoms are small. In such materials the overlap of atomic orbitals and potentials on neighbouring atoms is relatively large. In that case the wave function of the electron can be approximated by a (modified) plane wave. The band structure of a metal like Aluminum even gets close to the Empty Lattice Approximation.
Tight binding model
The opposite extreme to the nearly-free electron approximation assumes the electrons in the crystal behave much like an assembly of constituent atoms. This tight binding model assumes the solution to the time-independent single electron Schrödinger equation 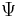 is well approximated by a linear combination of atomic orbitals
is well approximated by a linear combination of atomic orbitals 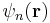 .[2]
.[2]
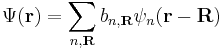 ,
,
where the coefficients 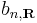 are selected to give the best approximate solution of this form. Index n refers to an atomic energy level and R refers to an atomic site. A more accurate approach using this idea employs Wannier functions, defined by:[3][4]
are selected to give the best approximate solution of this form. Index n refers to an atomic energy level and R refers to an atomic site. A more accurate approach using this idea employs Wannier functions, defined by:[3][4]
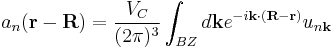 ;
;
in which 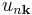 is the periodic part of the Bloch wave and the integral is over the Brillouin zone. Here index n refers to the n-th energy band in the crystal. The Wannier functions are localized near atomic sites, like atomic orbitals, but being defined in terms of Bloch functions they are accurately related to solutions based upon the crystal potential. Wannier functions on different atomic sites R are orthogonal. The Wannier functions can be used to form the Schrödinger solution for the n-th energy band as:
is the periodic part of the Bloch wave and the integral is over the Brillouin zone. Here index n refers to the n-th energy band in the crystal. The Wannier functions are localized near atomic sites, like atomic orbitals, but being defined in terms of Bloch functions they are accurately related to solutions based upon the crystal potential. Wannier functions on different atomic sites R are orthogonal. The Wannier functions can be used to form the Schrödinger solution for the n-th energy band as:
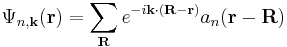 .
.
The TB model works well in materials with limited overlap between atomic orbitals and potentials on neighbouring atoms. Band structures of materials like Si, GaAs, SiO2 and diamond for instance are well described by TB-Hamiltonians on the basis of atomic sp3 orbitals. In transition metals a mixed TB-NFE model is used to describe the broad NFE conduction band and the narrow embedded TB d-bands. The radial functions of the atomic orbital part of the Wannier functions are most easily calculated by the use of pseudopotential methods. NFE, TB or combined NFE-TB band structure calculations,[5] sometimes extended with wave function approximations based on pseudopotential methods, are often used as an economic starting point for further calculations.
KKR model
The simplest form of this approximation centers non-overlapping spheres (referred to as muffin tins) on the atomic positions. Within these regions, the potential experienced by an electron is approximated to be spherically symmetric about the given nucleus. In the remaining interstitial region, the screened potential is approximated as a constant. Continuity of the potential between the atom-centered spheres and interstitial region is enforced.
A variational implementation was suggested by Korringa and by Kohn and Rostocker, and is often referred to as the KKR model.[6][7]
Order-N spectral methods
To quote RP Martin: "The concept of localization can be imbedded directly into the methods of electronic structure to create algorithms that take advantage of locality … For large systems, this fact can be used to make "order-N" or O(N) methods where the computational time scales linearly in the size of the system".[8][9][10]
Density-functional theory
In recent physics literature, a large majority of the electronic structures and band plots are calculated using density-functional theory (DFT), which is not a model but rather a theory, i.e., a microscopic first-principles theory of condensed matter physics that tries to cope with the electron-electron many-body problem via the introduction of an exchange-correlation term in the functional of the electronic density. DFT-calculated bands are in many cases found to be in agreement with experimentally measured bands, for example by angle-resolved photoemission spectroscopy (ARPES). In particular, the band shape is typically well reproduced by DFT. But there are also systematic errors in DFT bands when compared to experiment results. In particular, DFT seems to systematically underestimate by about 30-40% the band gap in insulators and semiconductors.
It must be said that DFT is, in principle an exact theory to reproduce and predict ground state properties (e.g., the total energy, the atomic structure, etc.). However, DFT is not a theory to address excited state properties, such as the band plot of a solid that represents the excitation energies of electrons injected or removed from the system. What in literature is quoted as a DFT band plot is a representation of the DFT Kohn-Sham energies, i.e., the energies of a fictive non-interacting system, the Kohn-Sham system, which has no physical interpretation at all. The Kohn-Sham electronic structure must not be confused with the real, quasiparticle electronic structure of a system, and there is no Koopman's theorem holding for Kohn-Sham energies, as there is for Hartree-Fock energies, which can be truly considered as an approximation for quasiparticle energies. Hence, in principle, Kohn-Sham based DFT is not a band theory, i.e., not a theory suitable for calculating bands and band-plots. In principle time-dependent DFT can be used to calculate the true band structure although in practise this is often difficult.
Green's function methods and the ab initio GW approximation
To calculate the bands including electron-electron interaction many-body effects, one can resort to so-called Green's function methods. Indeed, knowledge of the Green's function of a system provides both ground (the total energy) and also excited state observables of the system. The poles of the Green's function are the quasiparticle energies, the bands of a solid. The Green's function can be calculated by solving the Dyson equation once the self-energy of the system is known. For real systems like solids, the self-energy is a very complex quantity and usually approximations are needed to solve the problem. One such approximation is the GW approximation, so called from the mathematical form the self-energy takes as the product Σ = GW of the Green's function G and the dynamically screened interaction W. This approach is more pertinent when addressing the calculation of band plots (and also quantities beyond, such as the spectral function) and can also be formulated in a completely ab initio way. The GW approximation seems to provide band gaps of insulators and semiconductors in agreement with experiment, and hence to correct the systematic DFT underestimation.
Mott insulators
Although the nearly-free electron approximation is able to describe many properties of electron band structures, one consequence of this theory is that it predicts the same number of electrons in each unit cell. If the number of electrons is odd, we would then expect that there is an unpaired electron in each unit cell, and thus that the valence band is not fully occupied, making the material a conductor. However, materials such as CoO that have an odd number of electrons per unit cell are insulators, in direct conflict with this result. This kind of material is known as a Mott insulator, and requires inclusion of detailed electron-electron interactions (treated only as an averaged effect on the crystal potential in band theory) to explain the discrepancy. The Hubbard model is an approximate theory that can include these interactions. It can be treated non-perturbatively within the so-called Dynamical Mean Field Theory, which bridges the gap between the nearly-free electron approximation and the atomic limit.
Augmented plane waves
John Clarke Slater and members of his Solid State and Molecular Theory Group in the Physics Department at MIT, comprised one of the main research centers for the calculation of band structures.[11] John Wood played a very strong role in large scale computations using the augmented plane wave (APW) method.[12]
Others
Calculating band structures is an important topic in theoretical solid state physics. In addition to the models mentioned above, other models include the following:
- k·p perturbation theory is a technique that allows a band structure to be approximately described in terms of just a few parameters. The technique is commonly used for semiconductors, and the parameters in the model are often determined by experiment.
- The Kronig-Penney Model, a one-dimensional rectangular well model useful for illustration of band formation. While simple, it predicts many important phenomena, but is not quantitative.
- Hubbard model
The band structure has been generalised to wavevectors that are complex numbers, resulting in what is called a complex band structure, which is of interest at surfaces and interfaces.
Each model describes some types of solids very well, and others poorly. The nearly-free electron model works well for metals, but poorly for non-metals. The tight binding model is extremely accurate for ionic insulators, such as metal halide salts (e.g. NaCl).
References
- ^ Kittel, p. 179
- ^ Kittel, pp. 245-248
- ^ Kittel, Eq. 42 p. 267
- ^ Daniel Charles Mattis (1994). The Many-Body Problem: Encyclopaedia of Exactly Solved Models in One Dimension. World Scientific. p. 340. ISBN 9810214766. http://books.google.com/books?id=BGdHpCAMiLgC&pg=PA332&dq=wannier+functions#PPA340,M1.
- ^ Walter Ashley Harrison (1989). Electronic Structure and the Properties of Solids. Dover Publications. ISBN 0-486-66021-4. http://books.google.com/books?id=R2VqQgAACAAJ.
- ^ Joginder Singh Galsin (2001). Impurity Scattering in Metal Alloys. Springer. Appendix C. ISBN 0306465744. http://books.google.com/books?id=kmcLT63iX_EC&pg=PA498&dq=KKR+method+band+structure.
- ^ Kuon Inoue, Kazuo Ohtaka (2004). Photonic Crystals. Springer. p. 66. ISBN 3540205594. http://books.google.com/books?id=GIa3HRgPYhAC&pg=PA66&dq=KKR+method+band+structure.
- ^ Richard M Martin (2004). Electronic Structure: Basic Theory and Practical Methods. Cambridge University Press. Chapter 23. ISBN 0521782856. http://books.google.com/books?id=dmRTFLpSGNsC&pg=PA316&dq=isbn=0521782856#PPA450,M1.
- ^ P. Ordejon (1998). "Order-N tight-binding methods for electronic-structure and molecular dynamics". Computational Materials Science 12 (3): 157. doi:10.1016/S0927-0256(98)00027-5.
- ^ Richard M Martin Linear Scaling ‘Order-N’ Methods in Electronic Structure Theory
- ^ Philip M. Morse, John Clarke Slater, 1900-1976: A biographical memoir, National Academy of Sciences, National Academy Press on-line
- ^ Paul Hoch and Krzysstof Szymborski, The development of the band theory of solids in Lillian Hoddeson, Ernest Braun, Jurgen Teichmann and Spencer Weart, Out of the crystal maze: chapters from the history of solid state physics, Oxford University Press, Oxford, 1992. page 205.
Bibliography
- Charles Kittel (1996). Introduction to Solid State Physics (Seventh Edition ed.). New York: Wiley. ISBN 0-471-11181-3. http://worldcat.org/isbn/0471111813.
Further reading
- Microelectronics, by Jacob Millman and Arvin Gabriel, ISBN 0-07-463736-3, Tata McGraw-Hill Edition.
- Solid State Physics, by Neil Ashcroft and N. David Mermin, ISBN 0-03-083993-9
- Elementary Solid State Physics: Principles and Applications, by M. Ali Omar, ISBN 0-201-60733-6
- Electronic and Optoelectronic Properties of Semiconductor Structures - Chapter 2 and 3 by Jasprit Singh, ISBN 0-521-82379-X
- Electronic Structure: Basic Theory and Practical Methods by Richard Martin, ISBN 978-052178285
- Condensed Matter Physics by Michael P. Marder, ISBN 0-471-17779-2
- Computational Methods in Solid State Physics by V V Nemoshkalenko and N.V. Antonov, ISBN 90-5699-094-2
- Elementary Electronic Structure by Walter A. Harrison, ISBN 981-238-708-0
- Pseudopotentials in the theory of metals by Walter A. Harrison, W.A. Benjamin (New York) 1966
- Tutorial on Bandstructure Methods by Dr. Vasileska(2008)